Reaktive bzw. Resonanzabsorber
Im Gegensatz zu den vorherigen porösen, passiven Absorbern, tritt die Gruppe der reaktiven Absorber mit der auftreffenden Schallwelle in Wechselwirkung. Sie beeinflussen nicht nur den Pegel, sondern auch die Struktur der Schallfelder in ihrer Nähe und können sich auch, wenn sie sich nah beieinander befinden, gegenseitig beeinflussen (Müller/Möser 2004, S.258).
Im vorherigen Kapitel über passive Absorber wurde erwähnt, dass die Masse etwaiger Abdeckungen klein sein muss, um den Eintritt des Schalls in das absorbierende Material möglichst wenig zu beeinflussen. Bei den Resonanzabsorbern versucht man diese Beeinflussung gezielt auszunutzen. Die flächenbezogene Masse einer schwingenden Platte eines sogenannten Plattenschwingers wird also hierfür groß gewählt in Bezug auf die in der Schallwelle mitbewegte Luftmasse nach
Gleichung 5.2.1.i
und
Gleichung 2.4.a
(Müller/Möser 2004, S.259).
„Eine solche Masse kann mit dem Schallfeld nur reagieren, wenn sie als Teil eines Resonanzsystems anregbar gemacht wird.“
Alle dünnen aber dichten Materialien wie Gipskarton, Glas und Holz, aber auch dichte Folien oder Leder sind dafür geeignet (Fasold/Veres 2003, S. 83).
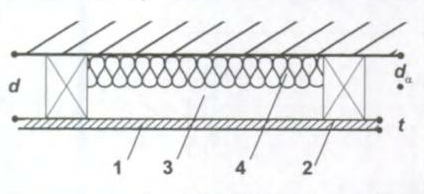
Plattenschwinger
1 - geschlossene Schicht der Masse m'' und Dicke t
2 - ein als starr angenommener Rahmen
3 - rundum geschlossenes Luftkissen der Dicke d [mm]
4 - locker eingelegte Dämpfungsschicht der Dicke dα [mm]
Das Luftvolumen hinter der Platte wirkt dabei als Feder hinter der schwingenden Plattenmasse. Damit die Platten frei schwingen können, muss eine Mindestgröße der frei schwingenden Fläche eingehalten werden. Diese Mindestgröße liegt in etwa bei 0,4m2. Der Abstand zwischen den Befestigungen sollte mindesten 0,5m betragen (Fasold/Veres 2003, S.83). Auch wenn man diese Mindestmaße einhält, muss man bedenken, dass viele Unsicherheiten im Aufbau eines solchen Absorbers vorhanden sind, die die Berechnung im Vorfeld erschweren bzw. ungenau werden lassen, wie etwa die Aufhängung und das Biegeverhalten der Platte. So liegen zum Beispiel auch die Formeln für die Berechnung der Resonanzfrequenz dieses Feder-Masse-Schwingers aus den beiden Büchern (Fasold/Veres 2003) und (Müller/Möser 2004) um immerhin eine kleine Terz auseinander.
m' - flächenbezogene Masse in kg/m2
dL - Abstand zwischen Plattenrückseite und Wand in cm
m'' - flächenbezogene Masse in kg/m2
d - Dicke des rundum geschlossenen Luftkissens
F0 und fR entsprechen dabei in beiden Fällen der Resonanzfrequenz. Sie werden in den beiden zitierten Werken nur unterschiedlich benannt.
Auch bei dieser Art von Absorbern gilt, dass der Kennwiderstand nah an der Schallkennimpedanz Z0 der Luft liegen muss, um einen hohen Absorptionsgrad zu erreichen.
„Die optimale Auslegung eines Feder-Masse-Systems erfolgt vor allem durch die Wahl des Kennwiderstandes Z'R. Die für breitbandige Absorption wichtigste Auslegungsregel besteht demnach darin, sowohl m'' als auch s'' – unabhängig vom jeweiligen fR – möglichst klein zu wählen.“
Große Massen alleine kennzeichnen also noch keinen optimalen Resonanzabsorber. Mit der größeren Masse steigt auch die Resonanzschärfe.
Die Größe von s'', also die Federsteife hinter der Platte, wird vorwiegend über den Wandabstand bestimmt. Doch auch für diesen gibt es Grenzen. Er darf weder zu groß noch zu klein im Verhältnis zur Wellenlänge sein.
Generell sollte man also versuchen, über das Ausnutzen des maximalen Wandabstand bis λ/12 und über kleine Massen an ein kleines ZR zu kommen, doch dagegen spricht die zentrale Auslegungsregel nach
Gleichung 5.2.2.a
bzw
Gleichung 5.2.2.b
. Daher wirken diese Tiefenabsorber auch nur schmalbandig oder mit einem maximalen Absorptionsgrad von unter 0,5 (Müller/Möser 2004, S.261).
teff - effektive Plattendicke (siehe die Erläuterungen nach Gleichung 5.2.1.j)
ε - Lochflächenverhältnis
Sie schwingt ebenfalls vor der Feder des dahinter liegenden Luftvolumens. Es gelten ebenfalls die Berechnungsformeln ab
Gleichung 5.2.2.a
.
Ein einzelnes solches Loch funktioniert als Helmholtzresonator wie die im Kapitel über die Raummoden erwähnten Gefäße von Hermann von Helmholtz. Ein solcher Resonator besteht aus dem Resonatorhals, in dem die Luftmasse schwingt und einem Resonatorvolumen, dessen eingeschlossene Luft als Feder wirkt. Es ist möglich, größere Volumina mit einer Öffnung als genau abgestimmten Tieftonabsorber zu planen (Fasold/Veres 2003, S.87)
Die Resonanzfrequenz berechnet sich hierfür zu
S - Fläche des Resonatorhalsquerschnittes in cm²
V - Resonatorvolumen in cm³
t - Resonatorhalslänge in cm (bzw. Materialdicke, wenn der Hals nur ein Loch in der Resonatorwand ist)
2Δt - Mündungskorrektur in cm
Die Mündungskorrektur entspricht bei einzelnen, runden Löchern etwa 0,8d (d = Durchmesser des Loches) und bei quadratischen Öffnungen etwa 0,9a (a = Seitenlänge des Loches). Bei schlitzförmigen Öffnungen von Resonatoren ist nicht nur die Schlitzgeometrie ausschlaggebend für die Mündungskorrektur, sondern auch die Resonanzfrequenz.
Mündungskorrektur für schlitzförmige Helmholtzresonatoren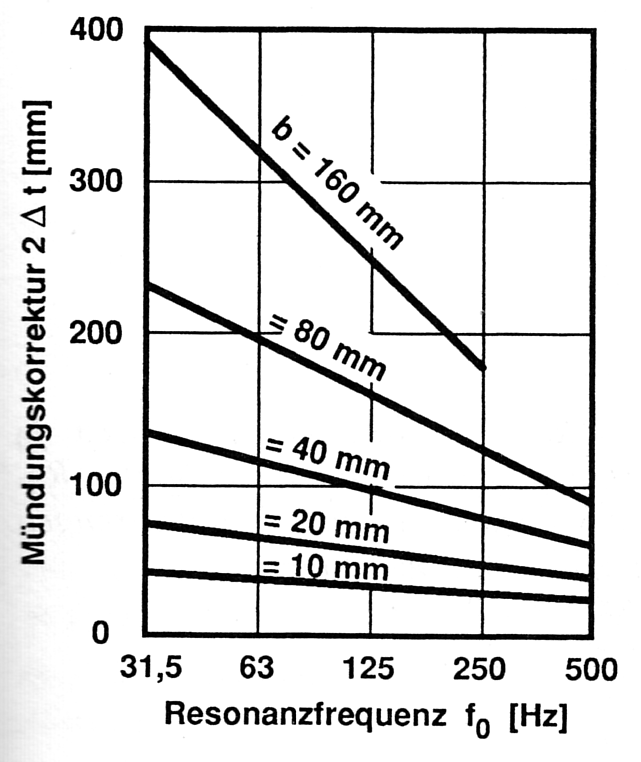
Die beste Absorption erreicht man vor allem mit großen Volumina, was folgende Abbildung recht anschaulich aufzeigt.
Auslegung von Helmholtzresonatoren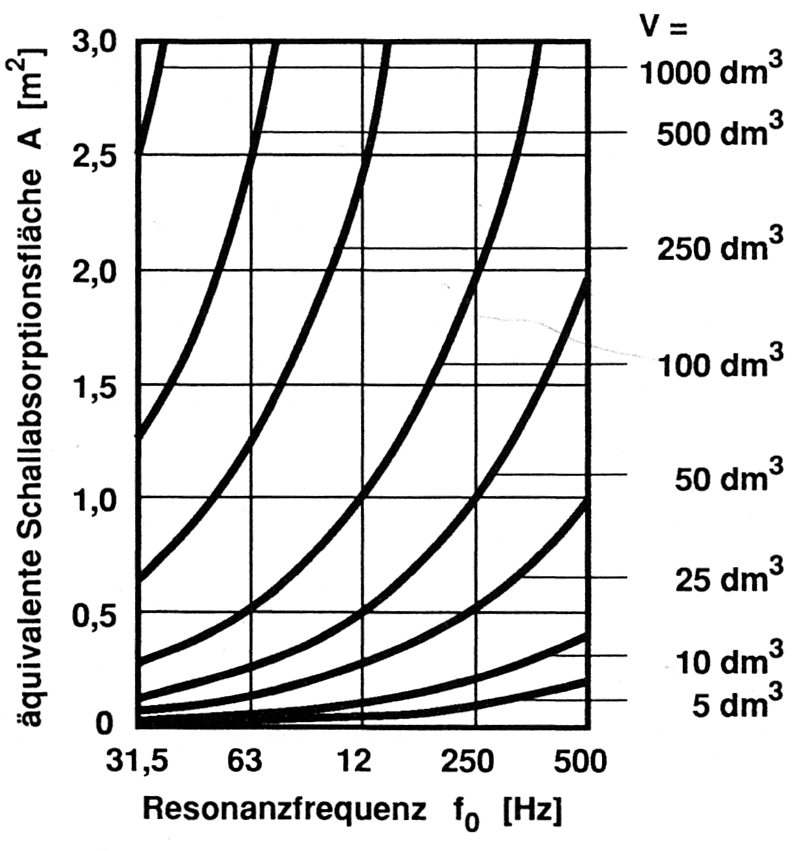
„Anders als beim Plattenresonator, kann man die Dämpfung dieses Schwingsystems „Luft in Luft“ - auch nach herkömmlicher Vorstellung – nicht nur durch eine lockere Füllung des Hohlraumes mit Dämpfungsmaterial, sondern sogar viel effizienter durch Aufspannen eines nach Gl. (9.28) optimalen Strömungswiderstands unmittelbar vor oder hinter den Löchern in Form zB. eines Faservlieses oder Tuches bewerkstelligen.“(Die im Zitat erwähnte Gleichung 9.28 entspricht Gleichung 5.2.1.g
Ohne jegliches poröses Material kommt man aus, wenn man die Lochabmessung so klein wählt, dass man in den Größenbereich der akustischen Zähigkeitsgrenzschicht kommt:
Die Reibung in den Löchern dieser mikroperforierten Absorber ist dann auch ohne zusätzliches Dämpfungsmaterial groß genug.
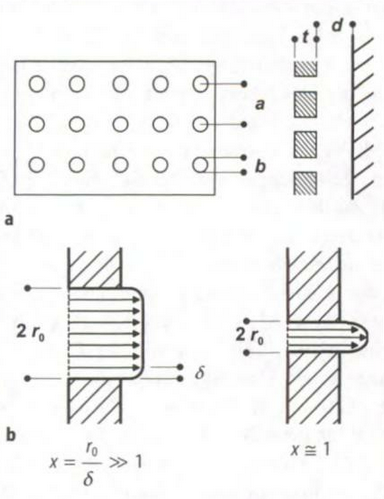
Mikroperforierte Platten und Folien
Oben: schematische Draufsicht und Schnitt
Unten: Schnelleverteilung in großen und kleinen Löchern oder Schlitzen
Es gibt sowohl mikroperforierte Platten als auch mikroperforierte Folien. Dabei ist die akustische Wirksamkeit fast unabhängig vom verwendeten Material, was zum Beispiel den Bau durchsichtiger Absorber aus Glas ermöglicht (Müller/Möser 2004, S.285).
Das Lochflächenverhältnis ist mit etwa 1% sehr klein. Bei Folien mit einem Lochdurchmesser in der Größe der Foliendicke kommt man trotzdem auf etwa 250.000 Löcher/m2 (Müller/Möser 2004, S.290). Es ist auch möglich zwei oder drei verschiedene mikroperforierte Schichten mit vorzugsweise wachsendem Abstand hintereinander anzubringen, um eine breitbandigere Wirkung zu erzielen (Müller/Möser 2004, S.289).
Da die schallabsorbierende Wirkung, vor allem in den mittleren und hohen Frequenzen, unabhängig von einem geschlossenen Luftvolumen hinter der perforierten Schicht ist, können auch (transparente) Streifen als Deckensegel oder einfach herabhängend aufgehängt werden. Die Schallabsporption ist dabei in jedem Fall höher als bei gleicher Anordnung aus Vlies oder Stoff (Müller/Möser 2004, S.292).
Besonders interessant ist der Einsatz mikroperforierter Materialien überall dort, wo Hygienevorschriften oder Feuchtigkeit bzw. Verschmutzung in der Luft (Lüftung) den Einsatz von porösen Materialien erschweren (Müller/Möser 2004, S.293).
