Passive bzw. Poröse Absorber
Der Schall soll bei dieser Art von Absorbern, in das Material aus Fasern oder offenzelligen Schäumen eindringen und dort einen Widerstand erfahren.
„Die Schallabsorption beruht auf der Wirkung der sehr dünnen Zähigkeitsgrenzschicht an der Oberfläche der Porositäten eines Körpers, an dem ein Schallfeld anliegt (das sind beim porösen Absorber die kleinen Hohlräume und Kanäle).Die Dicke der Grenzschicht d (ebene Körperoberfläche), in der die Schallschnelle des Fluids bis auf den Wert Null an der Wand abfällt, beträgt etwa
Die Dissipation infolge dieser Zähigkeitswirkung in der Grenzschicht ist relativ gering. Sie wächst aber zu beachtlicher Größe an, wenn durch die aufgelockerte, poröse Gestaltung der Oberfläche (z.B. durch eine extreme Oberflächenvergrößerung mit Hilfe eines gestopften Fasermaterials, eines offenporigen Schaumstoffes oder eines porösen Betons) die Dissipation an sehr großen Flächen erfolgt.“ (DEGA 2006, S.40)
Diese Absorber „...bezeichnet man als passiv, weil sie – trotz ihres in der Regel sehr niedrigen Raumgewichtes ρa ≥60 kg/m3 - von Schallwellen praktisch nicht zum Mitschwingen angeregt werden. Ihre Strukturen – so zerbrechlich und empfindlich sie gegenüber mechanischer Beanspruchung auch sein mögen – sind i.Allg. schwer genug, um von beliebigen Luftschallfeldern im Hörbereich nicht mitbewegt zu werden.“
Diese Gruppe von Absorbern schluckt also Schallenergie, ohne selbst „aktiv“ zu werden.
Die ausschlaggebenden Materialeigenschaften für die benutzen Materialien sind die Porosität s, der Strukturfaktor Χ und der spezifische Strömungswiderstand Rs (Müller/Möser 2004, S.251).
Die Porosität s ist der Anteil des akustisch wirksamen Luftvolumens VL am Gesamtvolumen des Absorbers VA.
Der Strukturfaktor Χ ist das Verhältnis zwischen dem an der Kompression beteiligten (VK) zu dem an der Beschleunigung beteiligten Volumen (VB) (Müller/Möser 2004, S.251)
bzw. wie Fasold es einfacher ausdrückt, dem gesamten Luftvolumen in den Poren zu dem am Absorptionsvorgang tatsächlich beteiligten (Fasold/Veres 2003, S.71). Fasold vergleicht das wirksame Volumen mit jenem durchgehender gerader Kanäle im Dämmstoff, den Rest beschreibt er als „Sackgassen“.Der spezifische Strömungswiderstand Rs schließlich beschreibt den Druckunterschied Δp vor und hinter dem Absorber bei gleichmäßigem Durchströmen von Luft mit der Geschwindigkeit u.
Dieser Strömungswiderstand nimmt mit der Dicke des Materials natürlich zu. Als dicken-unabhängige Materialkenngröße wird deshalb der längenbezogene Strömungswiderstand Ξ verwendet. Dieser ergibt sich aus dem spezifischen Strömungswiderstand Rs dividiert durch die Schichtdicke d:
Wie in der Einführung zur Absorption beschrieben, darf der Schallkennimpedanz-Unterschied vor und hinter einer Grenzfläche, hier die Oberfläche des porösen Absorbers, nicht zu groß werden, da der Schall sonst vermehrt reflektiert wird.
Andererseits benötigt der Vorgang der Wandlung in Wärme Widerstand im Material selbst. Als optimaler spezifischer Strömungswiderstand für Schallabsober hat sich der Bereich
bzw. herausgestellt (Müller/Möser 2004, S.251).Je dicker die Dämmstoffschicht ist, desto geringer muss also der längenbezogene Strömungswiderstand des Materials sein, um im Optimum zu bleiben. Für die Absorption niedriger Frequenzen sind daher niedrigere Strömungswiderstände, für hohe Frequenzen höhere längenbezogene Strömungswiderstände besser geeignet (Fasold/Veres 2003, S.73).
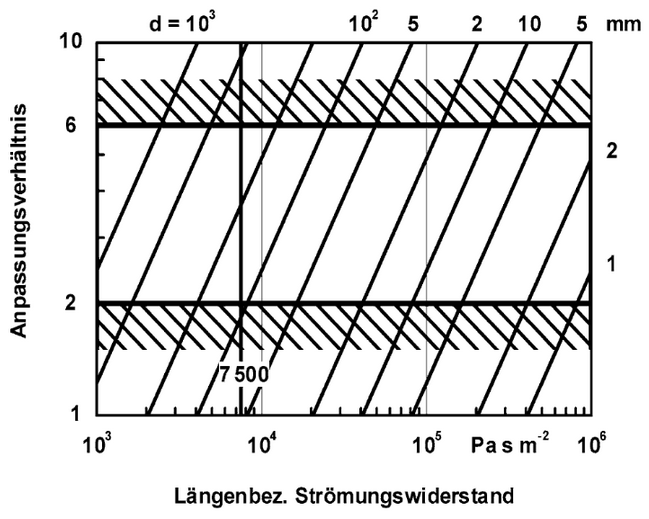
Anpassungsverhältnis ε als Funktion des längenbezogenen Strömungswiderstandes Ξ für verschiedene Schichtdicken.
Mit Hilfe dieses Diagramms kann die optimale Dicke eines porösen Materials mit einem vorgegebenen Strömungswiderstand, oder umgekehrt, der optimale Strömungswiderstand eines Absorbers mit vorgegebener Dicke ermittelt werden.
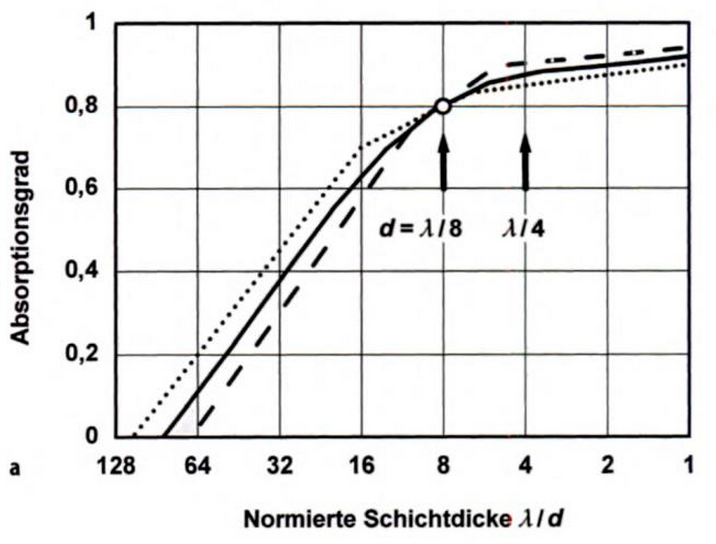
Auslegungshinweise für pöröse/fasrige Absorber mit optimalem Anpassungsverhältnis
ε = 2 (punktiert) bis 6 (strichliert) bei diffusem Schalleinfall.
Für rein senkrechten Schalleinfall liegen die erreichbaren Absorptionsgrade etwas tiefer.
Abdeckungen
Poröse Absorber werden oft gegen mechanische Beanspruchungen geschützt, zum Beispiel mit Lochplatten. Gegen Abrieb kann auch schon ein Tuch helfen. Oft wird vor den Dämmstoff auch ein „Rieselschutz“ gespannt, um das Verteilen von kleinen Fasern zu verhindern. Für diese Abdeckungen gilt, dass sie hinreichend schalltransparent sein müssen, um das Eindringen des Schalls in das Dämmmaterial nicht zu beeinträchtigen.
Der Strömungswiderstand eines Tuches addiert sich zu dem des Dämmstoffes und muss in Bezug auf den optimalen resultierenden Gesamtströmungswiderstand nach
Gleichung 5.2.1.g
gewählt werden. Eine Folie darf gegenüber der in der Schallwelle mitbewegten Luftmasse nicht zu schwer sein (Müller/Möser 2004, S.253).
m''F Masse der abdeckenden Folie,
m''A Masse der vom Schall mitbewegten Luft,
ρF flächenbezogene Masse der Folie,
t Dicke der Folie
Lochplatten sollten ein großes Lochflächenverhältnis ε aufweisen und dünn sein. Die Masse der mitschwingenden Luft in den Löchern ist ausschlaggebend für den Transmissionsgrad wie zuvor die flächenbezogene Masse der Folie (Müller/Möser 2004, S.254).
Bei der Halbwertsfrequenz f0,5 einer Lochplatte ergibt sich ein Schalltransmissionsgrad von 0,5.
Teff bezeichnet dabei die effektive Plattendicke. Sie besteht aus der eigentlichen Plattendicke, ergänzt um die Mündungskorrektur, die sich durch das Zusatzvolumen erklärt, welches beidseitig, nahe am Loch aber schon außerhalb, mitschwingt.
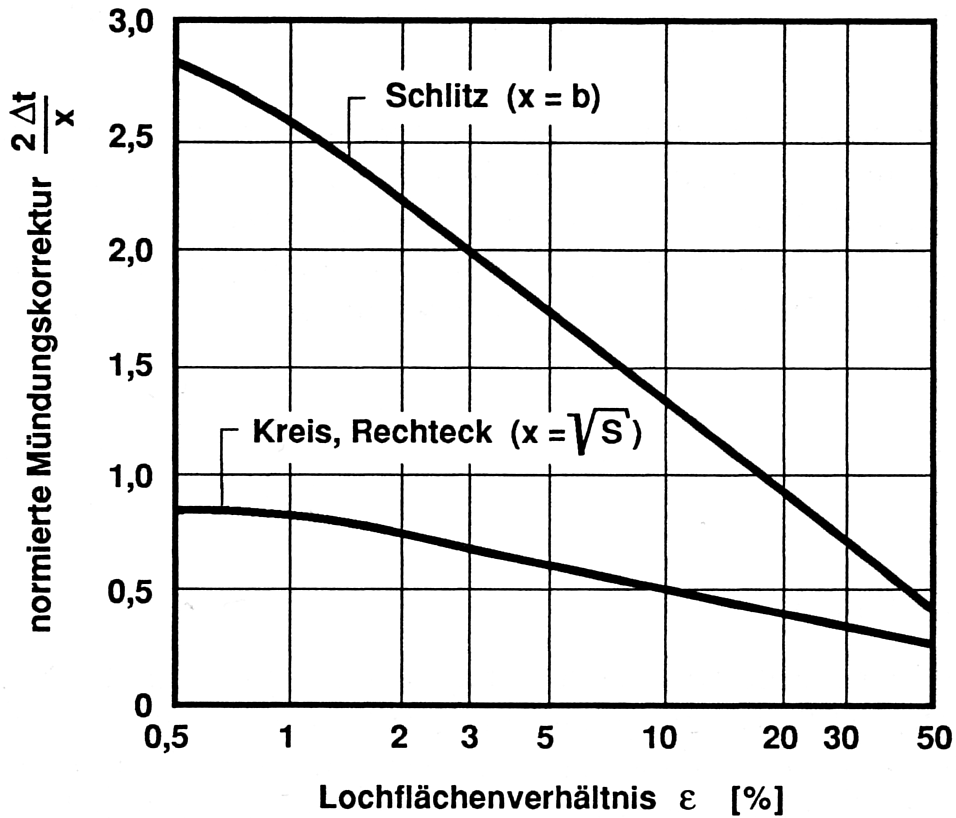
Δt steht für die Mündungskorrektur.
2 Δt ist die gesamte zusätzliche Korrekturlänge des Loches, da auf beiden Seiten der Öffnuung zusätzliches Luftvolumen mitschwingen kann.
Kreis: x ≈ 0.9d (d Durchmesser)
Quadrat: x = a (a Seitenlänge)
Rechteck: x = (a+b)/2 (a,b Seitenlängen)
Schlitz: x = b (b Schlitzbreite)
Die „...Mündungskorrektur, ist abhängig von der Lochgeometrie, aber auch vom Lochabstand (ausgedrückt beispielsweise durch das Lochflächenverhältnis), da sich die Öffnungen gegenseitig beeinflussen, und vom Wandabstand der Lochplatte...“ „Bei runden und quadratischen Öffnungen von 10mm Durchmesser oder Seitenlänge beträgt sie beispielsweise für Lochflächenverhältnisse von 20% etwa 4mm, bei Schlitzen von 10mm Breite für das gleiche Lochflächenverhältnis etwa 9mm. Der Einfluss der Mündungskorrektur erhöht sich mit kleiner werdendem Lochflächenverhältnis.“
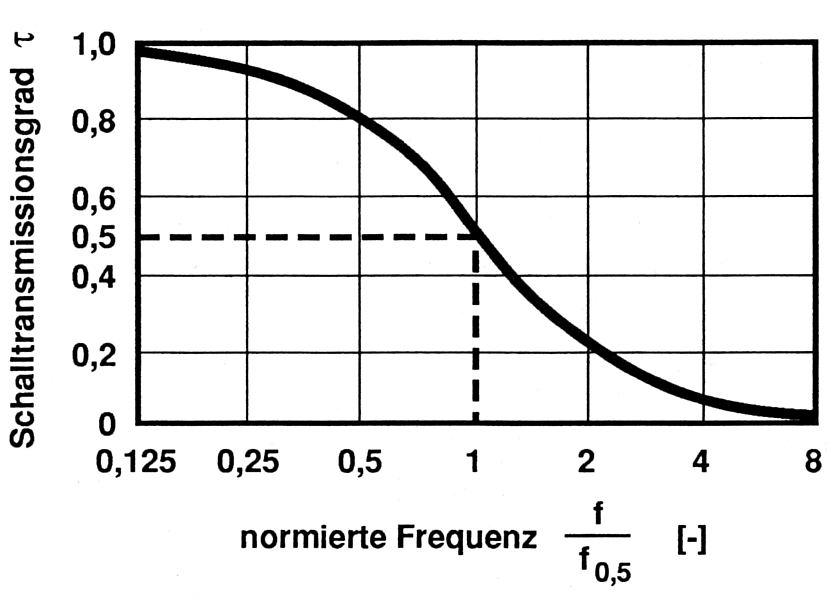
Der prinzipielle Frequenzverlauf des Transmissionsgrades normiert um die Halbwertsfrequenz.
Der resultierende Absorptionsgrad eines abgedeckten Dämmmaterials ergibt sich dann einfach aus dem Produkt des frequenzabhängigen Transmissionsgrades der Abdeckung und des frequenzabhängigen Absorptionsgrades des porösen Materials (ohne Abdeckung). (Fasold/Veres 2003, S.75)
